随着制造业对加工精度要求的不断提高, 近年来人们对进一步减小数控机床的误差进行了一系列探索. 研究表明, 在所有机床误差源中, 热误差比例高达60 % ~ 70 %[ 1] , 因此, 对数控机床热误差进行有效辨识和建模, 并实施补偿策略, 可以大幅提高加工精度。
针对误差补偿模型的研究从不同角度揭示了机床温度与热误差之间的关系. 常用的建模方法有: 最小二乘法拟合建模[ 2] , 基于多体系统理论的综合建模[ 3] , 时间序列分析建模[ 4] , 神经网络建模[ 5-8] , 灰色理论建模[ 9-10] 等, 其中神经网络和灰色模型是近年来应用较多的2 种机床热误差补偿模型. 机床的热误差预测模型是典型的、复杂的非线性系统, 影响因素繁多, 因此, 单一的建模方法虽然取得了一些成功应用, 但难以推广到其他结构的机床中去, 而且补偿精度也有待于进一步提高。
在分析灰色模型和神经网络2 种模型理论的基础上, 结合两者对数据处理的特点, 提出2 种不同结构的灰色神经网络预测模型: 并联型( Parallel GreyNeur al Netw o rk, PGNN ) 和嵌入型( Inlaid GreyNeur al Netw o rk, IGNN) . 在建立数学模型后, 将其用于实际工作状况下的机床热误差预测试验, 并且与传统的灰色模型和神经网络进行对比分析. 结果表明: 2 种结构的灰色神经网络模型预测结果符合预期目标, 无论是预测精度还是鲁棒性等指标均较传统模型有大幅提高。
1模型理论及分析
1. 1 GM( 1, N ) 预测模型理论
在使用灰色模型对机床热误差进行预测时, 首先需要利用已经获得的关键测点温度数据和热误差数据建立GM ( 1, N ) 模型. 设 ![]() 为热误差序列,
为热误差序列, ![]() 为关键温度测点的温度序列, 其中i= 2, 3,...,N , 表示该模型共选取了N - 1 个关键温度测点. 它们的一次累加生成序列为
为关键温度测点的温度序列, 其中i= 2, 3,...,N , 表示该模型共选取了N - 1 个关键温度测点. 它们的一次累加生成序列为
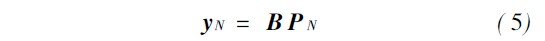
式中, n 为序列长度. 取![]() 序列相邻两项的平均值可生成序列:
序列相邻两项的平均值可生成序列:
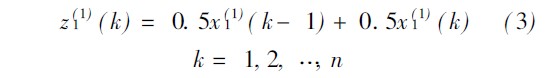
由此可建立GM( 1, N ) 模型:
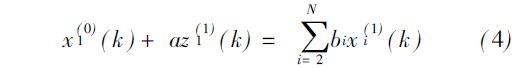
式中: a 为模型发展系数; bi 为灰作用量.
设式( 4) 中系数a 和b i 构成系数矢量:
![]()
由n- 1 项热误差数据构成的列矢量为
![]()
经过一次累加处理的热误差及温度数据构成矩阵:
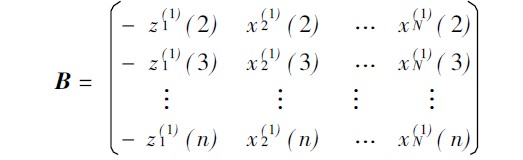
因此, 式( 4) 可表示为矩阵方程组:
![]()
根据最小二乘法原则, 可求出该模型的系数矢量:
![]()
根据灰色理论可知, GM( 1, N ) 的近似时间响应式可表示为
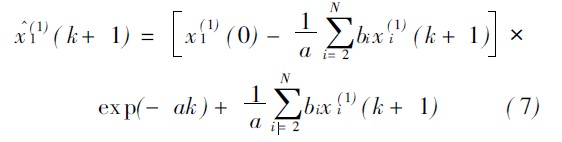
式中:![]()
将式( 6) 计算的系数矢量代入式( 7) 可得出![]() 序列, 通过
序列, 通过
![]()
一次累减还原, 就可得到GM ( 1, N ) 模型对于热误差的预测值.
1. 2 BP 神经网络预测模型理论
BP 神经网络是目前应用最广泛的一种神经网络, 具有非线性映射的特点, 其学习过程由正向数据传播和反向误差传播组成. BP 神经网络的输入层接收机床的温度数据, 因此, 选择的温度测点数量决定了输入层神经元节点的数量, 这里设定为n. 模型的输出为热误差预测值, 所以输出层有1 个节点. 隐藏层的节点数量往往根据经验确定[ 6-7] . 输出层的传递函数为线性函数. 输入层、隐藏层传递函数为Sigmoid型. 在对神经网络进行训练时, 采用梯度下降法不断修正各个神经元的阈值和权值, 直到网络输出精度符合预定要求为止.
1. 3 并联型灰色神经网络
PGNN 预测模型的思路是: 首先分别用GM( 1,N) 和BP 神经网络分别对机床热误差进行预测, 然后对预测结果适当有效组合作为实际预测值. 其原理如图1 所示.
PGNN 模型的实质是组合预测, 目的是综合利用各种建模方法所提供的信息, 避免单一模型丢失信息的缺憾, 提高综合预测精度. 若假设y ( t) 为t 时刻的实际测量值, 则线性组合公式可表示为
![]()
式中: y^( t) 为组合模型对y ( t) 的预测值;
y^1 ( t) 、y^2 ( t)分别为灰色模型和神经网络对y ( t) 的预测值; k1 ( t ) 、k2 ( t) 分别为灰色模型和神经网络的加权系数.
2 种单一模型的加权系数k1 ( t) 和k2 ( t ) 在任意时刻都必须满足下列条件:
k1 ( t) + k2 ( t) = 1 ( 10)
确定k1 ( t ) 和k2 ( t) 是关系到模型预测精度的重要问题[ 1] . 考虑到机床热误差补偿的实时性要求, 本文采用定权预测, 即k1 和k2 始终保持不变, 并根据有效度[ 11] 概念确定其具体数值.
根据上述假设, 可以定义预测模型在时刻t 的预测精度为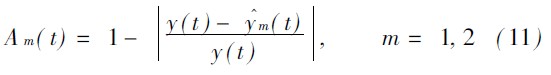
由A m( t) 构成模型的预测精度序列, 该序列的均值与均方差分别为
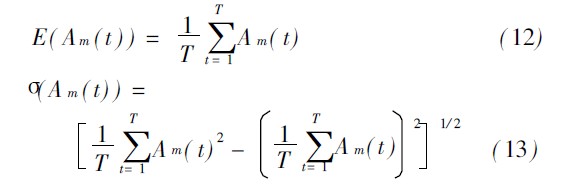
则预测模型的有效度可定义为
![]()
由式( 14) 可知, 预测模型的有效度S 越大, 其预测精度越高, 模型越有效. 文献[ 11] 中给出了对此近似求最优解的方法, 但是十分复杂. 本文使用一个计算简便且物理意义明确的方法确定加权系数k1 ,k2 . 由式( 11) ~ ( 14) 可分别求出灰色模型GM( 1,N ) 和神经网络的有效度S1、S 2 , 将其归一化处理后即可得到加权系数k1、k2 .

1. 4 嵌入型灰色神经网络
IGNN 借鉴了灰色理论思想对BP 神经网络的拓扑结构进行了改造, 旨在强化BP 神经网络对数据的处理能力: 加快运算速度, 增加鲁棒性, 增强模型的容错能力. IGNN 结构如图2 所示.在BP 神经网络的输入层前增加一个灰化层,其作用是将原始数据按照式( 1)、( 2) 做一次累加处理, 生成新的数据序列, 有效弱化原始数据的随机性. 由于一次累加序列是单调递增的, 有利于发挥BP 神经网络的非线性拟合作用, 网络的学习时间会大大减少, 在增加预测精度的同时也加快了收敛速度. 在输出层后增加一个白化层, 其作用则是按照式( 8) 对神经网络的输出数据做一次累减还原处理, 以最终得到IGNN 对机床热误差的预测值.
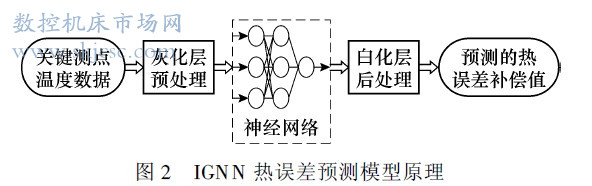
2 机床热误差测量试验
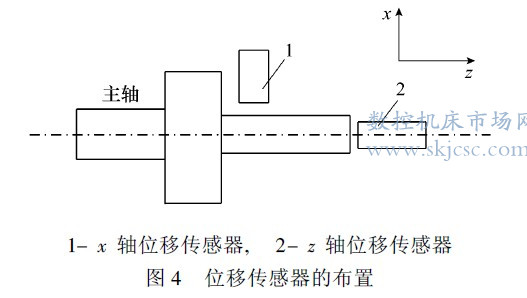
本试验在一台数控车削中心上进行温度和热误差数据采集. 在实际加工过程中, 机床的各个部件都会产生不同程度的温度变化, 有些对热误差影响较大, 有些影响甚微[ 10] . 为了优化试验过程和减少数据冗余, 如图3 所示, 本试验在机床的4 个关键位置布置温度传感器, 分别用于测量机床冷却液箱、x 轴螺母、机床主轴和机床床身的实时温度. 通常情况下, 高档数控机床的加工精度会受到环境温度变化的影响, 所以有必要实时测量机床所处的环境温度.
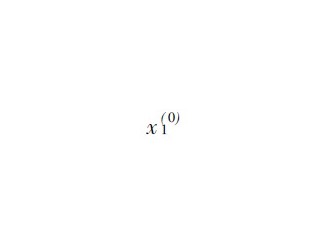
如图4 所示, 固定在床身的2 个位移传感器分别用于测量z 、x 轴方向的加工误差. 考虑文章篇幅, 本文仅对x 轴方向的热误差进行建模及说明, z轴方向的热误差可以采用相同方法.
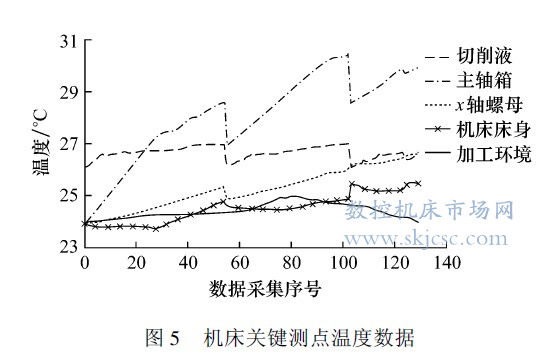
为了尽可能多地获得机床在各种加工条件下的温度和误差数据, 试验对多个加工过程( 机床运转-停机- 再运转- 再停机- 再运转) 进行测量, 每5min 进行1 次数据采集, 总共采集了130 组数据, 耗时650 min. 所得温度和误差数据如图5、6 所示.

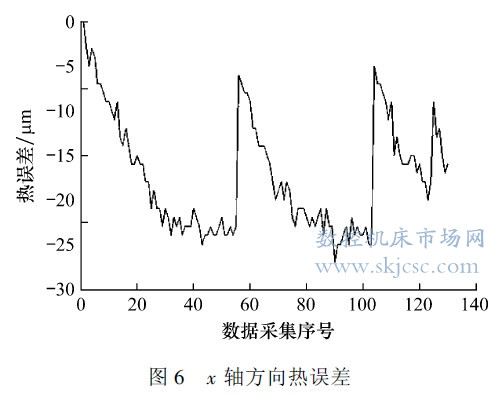
由图5、6 可见, 机床从冷态开始运转, 机床各部件温度变化较快, 热误差的变化速度也相应较快, 但当机床各部件达到热平衡状态时, 热误差不再继续增长, 而是维持在一定范围内波动; 停机一段时间后, 机床温度下降, 热误差随之减小; 机床再次运转后, 随着温度的再次上升, 热误差又逐渐增大, 随后机床再次进入热平衡状态, 热误差在小范围内波动.
3 模型建立及对比分析
为了验证PGNN 和IGNN 模型的有效性, 并且和单一灰色模型GM( 1, N ) 及BP 神经网络进行预测效果的比较, 本文采用48 组数据( 第56~ 103 组)对不同模型进行训练.
3. 1 GM( 1, N ) 模型建立
GM( 1, N ) 模型序列长度取6, 并采用等维滚动训练方法, 即每次预测一个机床热误差后, 将向该模型添加一组新数据, 去掉一组最老数据, 保持数据序列长度不变, 重新建模预测下一值. 模型中![]() 表示热误差值
表示热误差值 ![]() ( i= 2, 3, ..., 6) 分别表示5 个关键热源: 切削液、主轴箱、x 轴螺母、床身和环境温度,将其做一次累加处理后代入式( 3) ~ ( 6) , 求出灰色模型的系数矢量, 最后由式( 7)、( 8) 求出灰色模型预测的机床热误差数据.
( i= 2, 3, ..., 6) 分别表示5 个关键热源: 切削液、主轴箱、x 轴螺母、床身和环境温度,将其做一次累加处理后代入式( 3) ~ ( 6) , 求出灰色模型的系数矢量, 最后由式( 7)、( 8) 求出灰色模型预测的机床热误差数据.

3. 2 BP 模型建立
BP 神经网络预测模型的拓扑结构为5-8-1, 即输入层有5 个节点, 接收5 个关键热源的温度数据;隐藏层有8 个节点; 输出层有1 个节点, 输出机床热误差预测值. 由于输入层和隐藏层采用了Sigmoid函数, 其值域为[ 0, 1] , 为了提高网络收敛速度, 需要对温度数据进行规范化处理, 变换到[ 0, 1] 之间. 输出层采用线性传递函数. 设定学习速率为0. 01, 最大训练次数为12 *103 次. 学习目标取总误差为0. 01.
3. 3 PGNN 模型建立
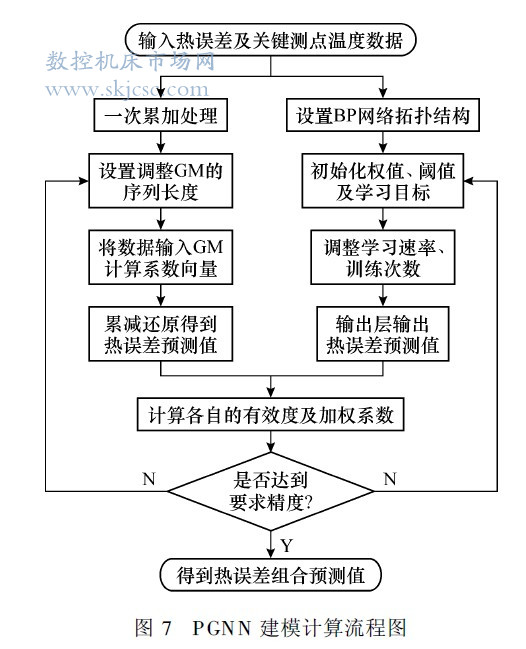
在该结构的组合预测模型中, 取BP 神经网络的结构为5-8-1, 其余参数设置同3. 2 节. 取GM( 1,N) 的序列长度为6, 同样采用等维滚动训练.由式( 11) ~ ( 14) 计算BP 神经网络和GM( 1,N) 的有效度分别为S 1= 0. 674, S2 = 0. 527. 因此,2 种单一预测模型的加权系数由式( 15) 计算可得k1= 0. 561, k2 = 0. 439. 将其代入式( 9) 可得PGNN的组合预测结果. 图7 所示为PGNN 模型的建模计算流程图.
3. 4 IGNN 模型建立
BP 神经网络前的灰化层将原始数据按式( 1) 、( 2) 作一次累加平滑预处理, 神经网络后的白化层对输出数据按照式( 8) 进行一次累减还原处理. 在该模型中, 神经网络的拓扑结构也取5-8-1, 其余参数设置同3. 2 节.
3. 5 模型验证及对比分析
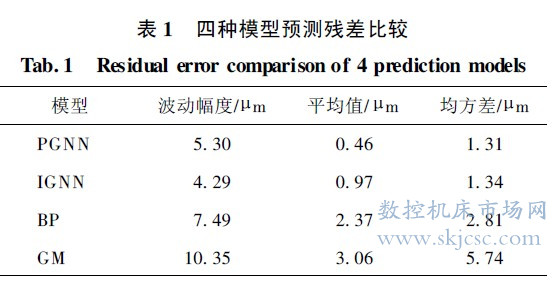
通过上述计算过程, 得到4 种不同的热误差预测模型. 下面用55 组数据( 第1~ 55 组) 进行模型验证. 图8所示为4种预测模型对实际热误差的拟合情况及及预测残差. 其中, 残差为实际热误差和模型预测结果做差值运算后得到.
由图8 可得:
( 1) 无论机床是否达到热平衡状态, 2 种结构的灰色神经网络模型预测效果均优于单一GM( 1,N ) 和BP神经网络模型. 说明组合预测模型至少是非劣性模型, 当事先无法预知模型预测效果时, 使用组合预测可以提高预测精度, 有一定的实用价值.
( 2) 在优化选取PGN N 模型的加权系数后, 可使其预测精度高于其他3 种模型, 残差平均值和方差是4 种模型中最小的, 且基本围绕零轴分布.
( 3) IGNN 模型和传统BP 相比多了灰化层和白化层, 减少了数据的随机性对模型预测精度的影响. 由图8( b) 可见, 由于受温度等外部环境突变的影响, 在第28 和第40 组试验数据处, BP 神经网络的残差绝对值远大于相同模型的其他点, 但IGNN的残差相对变化幅度较小, 起到了弱化数据随机性和降噪的效果.
( 4) 在机床未达到热平衡状态时, 机床各部件的温度处于不断变化的状态, 而且造成的热变形也不尽相同. 传统神经网络和灰色模型未能很好地反映这一快速变化的过程, 因此预测结果和实际情况有较大偏差. 随着温度不断升高, 直到机床基本处于热平衡状态时, 两者的预测精度有所提高, 但和组合灰色神经网络模型相比仍有一定差距.综上所述, 灰色神经网络预测模型在任何工况下都具有较高的预测精度, 至少可将数控机床加工精度提高约70% . 具体对比结果如表1 所示.
4结语
试验结果及模型比较表明, 2 种组合预测模型PGNN 和IGNN 由于结合了灰色理论和BP 神经网络优点, 有效避免了单一模型丢失信息的缺憾, 大幅提高了模型的预测精度. 相对于其他模型, 本文模型具有算法成熟、建模精度高、鲁棒性强, 且对原始数据数量要求低等优点, 适合作为复杂加工场合中的误差预测补偿模型.
来源:中国机床网 www.machine35.com
(责任编辑:)




